RandomNumbers: Difference between revisions
(→G4) |
|||
| Line 757: | Line 757: | ||
double x0 = rgen0->fire(); | double x0 = rgen0->fire(); | ||
double x1 = rgen1->fire(); | double x1 = rgen1->fire(); | ||
</pre> | |||
The two instances of RandGeneral differ in the way that they interpolate within a bin; rgen0 assumes | The two instances of RandGeneral differ in the way that they interpolate within a bin; rgen0 assumes | ||
a uniform density across the bin while rgen1 assumes a delta function at the lower edge. | a uniform density across the bin while rgen1 assumes a delta function at the lower edge. | ||
RandGeneral always returns a variate on ]0,1[ and it is the user's responsibility to transform | RandGeneral always returns a variate on <nowiki>]0,1[</nowiki> and it is the user's responsibility to transform | ||
this into the domain native to the distribution. | this into the domain native to the distribution. | ||
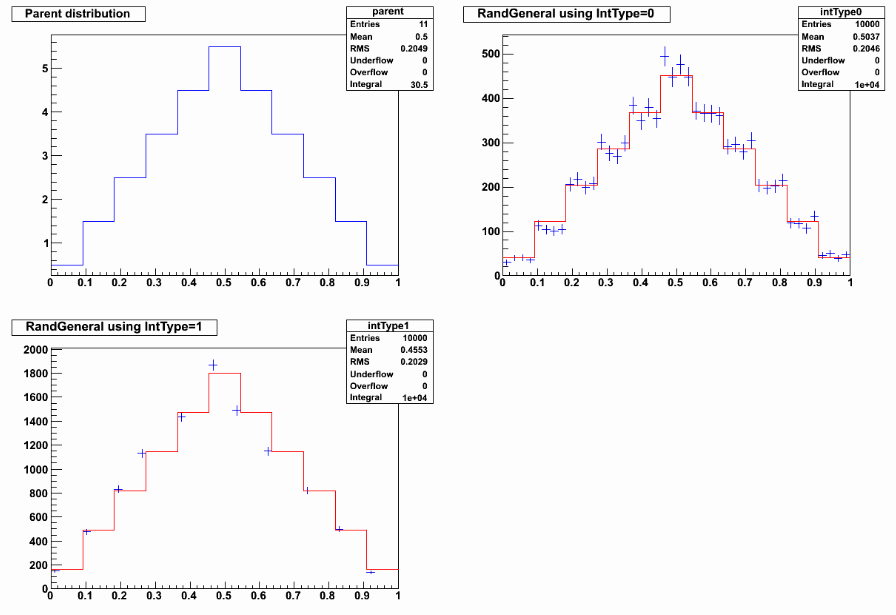
In the figure below, the upper left plot shows a histogram of the parent distribution from the code fragment above. | In the figure below, the upper left plot shows a histogram of the parent distribution from the code fragment above. | ||
In the upper right plot, the blue error bars show a binned histogram of the results | In the upper right plot, the blue error bars show a binned histogram of the results | ||
of 10,000 calls to rgen0->fire() | of 10,000 calls to <code>rgen0->fire()</code> this histogram has 44 bins, while the parent distribution had only 11. | ||
The error bars are sqrt(n). | The error bars are <code>sqrt(n)</code>. | ||
The parent distribution, scaled to 10,000 entries, is overlayed in red. In this figure one can see | The parent distribution, scaled to 10,000 entries, is overlayed in red. In this figure one can see | ||
that RandGeneral returns a constant density within each bin; it makes no attempt to smooth the distribution. | that RandGeneral returns a constant density within each bin; it makes no attempt to smooth the distribution. | ||
CLHEP does not provide a class that does a smoothed version of this, presumably because a fully general smoothing | CLHEP does not provide a class that does a smoothed version of this, presumably because a fully general smoothing | ||
algorithm is just too complicated. It is the user's | algorithm is just too complicated. It is the user's responsibility to choose fine enough bins for | ||
the job at hand. | the job at hand. | ||
In the lower left plot the blue error bars show a binned histogram of the results of 10,000 calls to | In the lower left plot the blue error bars show a binned histogram of the results of 10,000 calls to | ||
rgen1->fire() | <code>rgen1->fire()</code> this histogram has 44 bins. The parent distribution, scaled to 10,000 entries is overlayed in red. | ||
This illustrates that, when the IntType argument to the constructor of RandGeneral is set to 1, RandGeneral makes no | This illustrates that, when the <code>IntType</code> argument to the constructor of RandGeneral is set to 1, RandGeneral makes no attempt to interpolate within the bin and simply returns the lower edge of the bin. Careful inspection shows | ||
attempt to interpolate within the bin and simply returns the lower edge of the bin. Careful inspection shows | |||
that there is a bad interference between RandGeneral's notion of bin boundaries and the notion of bin boundaries | that there is a bad interference between RandGeneral's notion of bin boundaries and the notion of bin boundaries | ||
inside the | inside the histogramming package: the blue error bars are sometimes on the high side of the red vertical lines | ||
and sometimes on the low side. | and sometimes on the low side. | ||
[[File:RandGeneral.png|frame|Demonstrations of the effect different methods for drawing from a distribution.]] | |||
Notes for future developments. | Notes for future developments. | ||
==The Old Style Method for Getting Seeds== | ==The Old Style Method for Getting Seeds== | ||
Revision as of 15:40, 22 March 2017
Background
A typical Mu2e simulation job uses multiple independent sequences of pseudo-random numbers. The Mu2e Offline software and the art framework provide tools to create these sequences, to seed them, to save their state, to restore their state and to ensure that each random engine in a long chain of jobs has a unique seed. For some use cases it is important than two runs of the program use identical sequences of psuedo-random numbers; for other use cases it is important that the two runs of the program use unique sequences of pseudo-random numbers. This page discusses the tools available to help with this job and the standards and practices for using those tools.
The tools are two art services and one art module:
-
RandomNumberGenerator; an art service provided by art -
SeedService; an art service provided by Mu2e -
RandomNumberSaver; an art module provided by art
Basic Instructions
If all that you want to do is to run Mu2e jobs, not write Mu2e code, then you do not need to read this web page. You only to understand:
- How to edit fcl files to control the values of the random number seeds used by the art job
- How the mu2egrid scripts automatically do most of this for you.
This information is described on a page with self contained instructions for seeding the random number engines.
Introduction to CLHEP, Engines and Distributions
CLHEP (a Class Library for High-Energy Physics) is a general-purpose C++ library addressing several common needs of the HEP community. Its facilities are organized into packages; one such package, known as Random, provides well-known algorithms for the production and use of pseudo-random numbers. These algorithms are of two kinds, known respectively as engines and distributions.
Each of CLHEP's random number engines is designed such that, when called, it produces a value in which each bit is (ideally) as likely to be a 0 as to be a 1. In practice, the sequence of values produced by successive calls is based on an initial parameter, known as the engine's seed. When identically seeded, any two engines of the same type will produce the identical sequence of values, thus allowing for reproducible results.
A distribution is to take one or more values from a user-specified engine and to produce other values according to a function determined by the distribution's type and parameters. Each CLHEP distribution is designed to work with any of the CLHEP engines. Some of the distributions of interest to Mu2e are the flat, Gaussian and Poisson distributions.
See below for additional details specific to the CLHEP engines and distributions as used by Mu2e.
Mu2e will employ CLHEP's Random package for the foreseeable future.
In due course we will consider an adjustment allowing us to employ, as well, the random number facility
that is part of the C++11 standard library. (This facility is one of Fermilab's contributions to that standard.
See Clause 26.5 of the C++0X
Final Committee Draft.)
Introduction to the RandomNumberGenerator Service and the SeedService
It is an important Mu2e goal that code relying on random number generators produce results that can be reproduced when necessary. To aid in achieving this goal, the art framework provides a mechanism for the management of random number engines. Such management encompasses not only engine lifetime control (timely creation and destruction), but also engine seeding, saving, and restoring.
The mechanism is an art service known as the RandomNumberGenerator service.
It is Mu2e policy that each module requiring a random number engine employ this RandomNumberGenerator as described below.
A summary of the recommendations is:
- Do use the RandomNumberGenerator service to establish a random number engine when your module instance needs one.
- Do not instantiate your own random engine(s).
- Do not use the CLHEP singleton engine.
- Do not call any CLHEP functions that modify an engine's seeds.
- Do rely on the RandomNumberGenerator service to set seeds and to save and restore engines' state.
- Do use the SeedService service to obtain seeds for random engines.
- Do not use HepRandom; use RandFlat instead.
- Do not use RandPoisson; use RandPoissonQ instead.
- Do not use RandGauss; use RandGaussQ instead.
- Do not use the random bit functions of RandFlat; use RandBit instead
The only exception to these recommendations is when you are writing code that will only run
inside Geant4; in that case use the native Geant4 random number interfaces,
for example G4UniformRand() and G4RandGauss::shoot().
Repeatability
The ultimate goal of this discussion is to describe a methodology for using random number generators such that work is repeatable when it needs to be and is different when it needs to be. Several sorts of repeatability are important:
- Scenario 1: Run the same job, unchanged, twice. The same results should be obtained.
- Scenario 2:
- Run G4 and a hit making package in one job. Write out the output from both steps.
- In a separate job, read back the output of G4 and rerun the hit making package.
In this scenario, the output of the hit making package should be the same in both jobs.
- Scenario 3:
- Generate events 0 to 999 and save the state of the engine at the start of event 500.
- In a new job, set the engine to the saved state; generate events 500 to 999.
In this scenario, the events 500 to 999 should be the same in both cases.
Scenarios 1 and 2 are important for code development and debugging.
Scenario 3 is a powerful test to expose inadvertent use of uninitialized variables,
memory overwrites and other programming errors.
CLHEP engines
The CLHEP Random package provides a dozen engines,
each in the CLHEP namespace,
with varying speed-vs.-quality tradeoffs.
The list includes the Ranlux and Ranecu engines
from the earlier CERNLIB library,
as well as the commonly-used HepJamesRandom engine
whose algorithm was developed by Fred James
and described by him in Comp. Phys. Comm. 60 (1990) 329.
(Mu2e will probably use only the HepJamesRandom engine.)
For the most part,
CLHEP adopts the convention (as does Mu2e)
that the name of a source file corresponds to
the name of the class that it declares/defines.
For historical reasons,
a few CLHEP engine types do not obey this convention.
Note in particular that CLHEP::HepRandom is found in the file CLHEP/Random/Random.h, and CLHEP::HepJamesRandom is found in the file CLHEP/Random/JamesRandom.h.
All CLHEP engines share a common interface,
as defined by a base class (CLHEP::HepRandomEngine)
from which each of the other engine types inherits. For example,
the engine member function that produces a value
is consistently named fire().
Also, each engine can be seeded with a single value of type long
from the closed domain [0,900000000];
each value of the seed initializes the engine to a state
that will produce a unique and repeatable sequence
of pseudo-random uniform variates.
(The length of each unique sequence is much, much longer than we need.)
However, as recommended above, Mu2e modules should avoid any direct use of any CLHEP engine. Instead:
- Use the RandomNumberGenerator service from a module's constructor to establish (create and seed) one or more engines as the module may require, and
- Allow distributions to draw values, as needed, from these engines.
CLHEP distributions
The CLHEP Random package implements the following distributions,
each in the CLHEP namespace:
RandBinomial,RandBreitWigner,RandChiSquare,RandExponential,RandFlat,RandGamma,RandGauss,RandGeneral,RandLandau,RandPoisson, andRandStudentT.
Most of these names are likely self-explanatory;
the exception is RandGeneral,
which draws random variates from a binned representation of a function
(see <a href=#randgeneral>below</a> for details).
CLHEP Random also provides specializations
of some of the above distributions:
RandBit, a specialization ofRandFlat,RandGaussQandRandGaussT, both specializations ofRandGauss, andRandPoissonQandRandPoissonT, both specializations ofRandPoisson.
We recommend that Mu2e code use
RandGaussQ and RandPoissonQ
rather than other versions of the Gaussian and Poisson distributions.
We also recommend that, if random bits are wanted,
Mu2e code use the RandBit distribution,
rather than the random bit methods within RandFlat.
Our rationale is simply that
users of any non-recommended distributions
will need to do extra work in order to ensure reproducibility;
users of the recommended distributions need do no extra work.
The RandomNumberGenerator Service
Introduction
Via this RandomNumberGenerator service, the CLHEP random number engines are made available such that a client module may establish and subsequently employ any number of independent engines, each of any of the CLHEP engine types.
Any producer, analyzer, or filter module may freely use this Service as desired. However, by design, source modules are permitted to make no use of this Service.
Creating an engine
Each engine to be used by a module must be created in that module's constructor. Creating an engine involves specifying:
- An integer seed value to initialize the engine's state,
- The desired kind of engine
(
HepJamesRandomby default), and - A label string (empty by default).
Within a module, no two engines may share the identical label.
The above three items of information are supplied
in a single call to a function named createEngine().
Because two of the three items have defaults (and may therefore be omitted),
the call may take any of several forms;
the following three examples therefore have equivalent effect:
createEngine( seed )createEngine( seed, "HepJamesRandom" )createEngine( seed, "HepJamesRandom", "" )
As a convenience,
each such call returns a reference to the newly-created engine;
this is the same reference that would be returned
from each subsequent corresponding getEngine() call (see below).
Therefore, if it is convenient to do so,
the reference returned from a call to createEngine()
can be safely used right away as illustrated below.
If there is no immediate need for it,
this returned reference can instead be safely ignored.
Note that the createEngine()function
is implicitly available to any producer, analyzer, or filter module;
no additional header need be #included.
Here is an example of a recommended practice
in which the result of a createEngine() call
is used right away (arguments elided for clarity):
CLHEP::RandFlat dist( createEngine(...) );
Creating the global engine
CLHEP provides the notion of a global engine, and Geant4 makes use of this feature. It is recommended that the designated Geant4 module (and no other) should create this global engine.
The Service recognizes the notation "G4Engine"
to create the engine that is used by Geant4.
It is strongly recommended to ignore the resulting engine reference,
leaving exclusive future engine use to Geant4 itself:
createEngine( seed, "G4Engine" );
Obtaining a seed value
Mu2e requires that seeds passed as arguments to createEngine must be obtained from the SeedService, an art
service that was developed by Mu2e and is currently in the Mu2e code base. In the near future SeedService will
become part of the artextensions UPS package but it's public interfaces and the rules for configuring it will remain
unchanged.
The SeedService supports several different modes but Mu2e only uses one of them, the autoIncrement mode, which will be
described here. In this mode, the run time configuration requires two parameters,
a base seed value and a maximum number of seeds per art job.
When code requires a seed,
it calls the getSeed() member function of the SeedService.
On the first call to getSeed() with one art job,
it will return the value of the base seed.
On the second call it will return the value of the base seed plus one. And so on,
If the number of calls to getSeed() exceeds the maximum then the SeedService will throw an exception.
Instructions on how to configure the SeedService are available in instructions for seeding the random number engines.
An example of using the SeedSerivce is:
CLHEP::RandFlat flat( createEngine(art::ServiceHandle<SeedService>()->getSeed() ));
You might find it easier to read this as two lines, instead of one:
art::ServiceHandle<SeedService> seeds; CLHEP::RandFlat flat( createEngine( seeds->getSeed() ));
The RandomNumberGenerator service has helper functions to find seed values in the parameter set of a module however Mu2e does not use these functions. For completeness these are documented below.
Service handles
To gain general access to this RandomNumberGenerator service, a module uses the facilities of the Service subsystem. Thus, after including the RandomNumberGenerator service header, a variable definition such as the following will obtain a handle to this Service:
art::Service<art::RandomNumberGenerator> rng;
Thereafter, most functionality of this Service is available via this variable. All handles to this Service are equivalent; a client may define as many or as few handles as desired.
A module that has no need for this Service
need not obtain any such handle at all.
Similarly, a module that creates an engine
and makes use of the reference returned by the createEngine() call
will also likely need obtain no handle.
Accessing an engine
To obtain access to a previously-established engine (see above),
call the Service's getEngine() function.
The call takes a single argument,
namely the label that had been used when the engine was established.
If omitted, an empty label is used by default:
CLHEP::HepRandomEngine & engine = rng -> getEngine();
Note that the Service automatically knows which module is making the access request, and will return a reference to the proper engine for the current module, using the label to disambiguate if the module has established more than one engine.
Saving and Restoring State
At the start of each event, the RandomNumberGenerator service takes a snapshot of the state of each engine that it manages. Art supplies a producer module whose type is RandomNumberSaver that will copy the saved state from the RandomNumberGenerator service and will add that state to the event as a data product. To use the RandomNumberSaver module, follow the pattern in this .fcl fragment:
services : {
# Your other service parameter sets
RandomNumberGenerator : {}
}
physics : {
producers : {
# Your other producer parameter sets
randomsaver : {
module_type : RandomNumberSaver
}
}
t1 : [ randomsaver, (your other module labels ....) ]
trigger_paths : [ t1 ]
The module label for the RandomNumberSaver module
may occur anywhere in a trigger path, so long as you do not have filters that will cause art to skip that
module. So putting it first is probably a good idea; remember that you
are saving a snapshot taken before the event began, not a snapshot taken
at the end of the event.
The saved state of an engine is labeled with two pieces of
information: the label of the module that was active at the time of the
create engine call; and the label string, if any, from the call to
createEngine. We will call this two part name an engine-name.
To tell art to use the saved state of the random number engines put the following in your fcl file:
services : {
# Your other service parameter sets
RandomNumberGenerator : { restoreStateLabel : randomsaver }
}
The value of the parameter restoreStateLabel must be the module label
of the RandomNumberSaver module from the first job. Of course the
input file for the second job must be the output file written by the first job.
If a module instance uses random numbers and if that module instance is used in both the first and second jobs, it must have the same module label in both jobs. And, in the second job, the module must create all engines exactly as it did in the first job; in particular the module label numbers must be the same. A seed, either explcit or default, is still required to create an engine but the state created by that seed will be ignored. So any seed may be used in the second job.
When art reads the first event it will read the saved state of all random engines from the event; it will do so before any modules are called. For each engine created in the second job, it will look for saved state in the event, labeled by the engine-name. For each engine for which the service finds saved state, it will poke the engine to restore its state from the saved state. For each engine for which there is no saved sate, the service will leave the state unchanged.
There is a corollary of this explanation that you might considered weaknesses of the system:
- If you use an engine during your constructor or during your beginJob method, then there is no event in memory and no way to restore state. So you will use the state created at engine creation-time; this is not, in general, fully reproducible; for example if you skip events, the sequence of random numbers will certainly differ.
Examples
Examples of using random numbers can be found at:
- Offline/Sandbox/src/Random01_module.cc
- Offline/Sandbox/src/Random02_module.cc
- Offline/Sandbox/test/random01.fcl
- Offline/Sandbox/test/random02.fcl
- Offline/Sandbox/test/random03.fcl
- Offline/Sandbox/test/random04.fcl
To run the tests:
mu2e -c Sandbox/test/random01.fcl >& log.1 mu2e -c Sandbox/test/random02.fcl >& log.2 mu2e -c Sandbox/test/random03.fcl >& log.3 mu2e -c Sandbox/test/random04.fcl >& log.4 grep Event: log.1 | grep foo >& foo.1 grep Event: log.2 >& foo.2 grep Event: log.3 | grep foo >& foo.3 grep Event: log.1 | grep bar >& bar.1 grep Event: log.3 | grep bar >& bar.3 diff foo.1 foo.2 diff foo.1 foo.3 diff bar.1 bar.3
Random01_module.cc uses the SeedService to get a seed and the RandomNumberGenerator
Service to create an engine; it then uses the engine to create a CLHEP::Randflat distribution object.
At constructor time it prints out the seed. It fires RandFlat once per event and prints out the module label,
the event number and the value of the random variate.
Notice that the data member engine_ is a reference to an engine, not an engine object. This is a critical part of the design and the repeatability features will fail if the data member holds an engine by value.
The file random01.fcl runs two instances for the module for 10 events and writes out the saved state.
The two instances are named foo and bar. If you inspect random01.fcl, log.1 and log.2 you will
see that the seeds used by the two instances of the module have the expected values of 0 and 1.
The file random02.fcl reads the event-data file created by random01.fcl and tells the RandomNumberGenerator service
to restore the state of each engine the at the start of each event. It only runs one instance of
the Random01 module. It also changes the base seed from that used in random01.fcl, which you can verify by
looking at the seed value printed out in the constructor.
If you compare the files foo.1 and foo.2 you will find that they are identical.
The file random03.fcl reads the event-data file created by random01.fcl and tells the RandomNumberGenerator service
to restore the state of each engine the at the start of each event. It runs two instances of the Random01 module
but it skips the first 5 events. If you compare the log.3 with log.1, you will see that log.3 only has
printout for events 6 through 10 and
that the random numbers are identical to those produced, for the same events, in log.1. You can do this check
by diffing foo.1 against foo.3 and bar.1 against bar.3.
The file Random02_module.cc shows another way of initializing the RandFlat distribtion: the data members
seed_ and engine_ have been removed and RandFlat has been initialized in a single line.
The file also intializes a second instance of RandFlat using the same engine as was used to initialize the
first RandFlat object; this illustrates how to use getEngine(). The reference returned by
getEngine() is the same as the reference returned by the previous call to createEngine.
Below are a few additional notes on these examples:
- The class RandFlat has a other constructors that takes a pointer to an engine instead of a reference to an engine. These have a very, very different meaning. When RandFlat is given an engine by reference, it assumes that some external agent is responsible for managing the lifetime of the engine. When RandFlat is given an engine by pointer, it assumes that it should take over ownership of the engine and it will delete the engine in its destructor. This is a serious error because the RandomNumberGenerator service owns the engine.
- Be aware that a distriubtion may do significant work when it is constructed (RandFlat does not). In those cases construct the distribution once and keep it throughout the lifetime of the job, as is shown in these examples.
The CLHEP Random Package
Documentation about the CLHEP Random package can be found at:
Much of the detailed documentation can be found in comments in the header files, which are accessible via the code browser.
Both of these packages distinguish the idea of Random Engines from Random Distributions. A crude
distinction is that an engine provides a randomly distributed set of bits and a distribution uses
an engine to form random variates drawn from the advertised distribution. In practice the CLHEP engines return a
double that is uniformly distributed over the open interval ]0,1[. So, at a conceptual level, a CLHEP engine is
interchangeable with a distribution that returns a uniform random variate, such as RandFlat; the differences are
in the details of the public interface. In fact the fire() method of a default constructed RandFlat just calls its
underlying engine and returns. But RandFlat does have a richer public interface than does the underlying engine; for example the underlying engine can only ever return a random variate on ]0,1[ but RandFlat can, for example,
be asked return return a random variate on ]a,b[.
The following code fragment is taken from the header of the base class for an engine:
virtual double flat() = 0; // Should return a pseudo random number between 0 and 1 // (excluding the end points) virtual void flatArray(const int size, double* vect) = 0; // Fills an array "vect" of specified size with flat random values.
It shows the two main methods for drawing random variates from an engine.
When you instantiate a distribution object, you must give it an engine as an argument; in this sense the
distribution objects do not have the concept of a default engine. However the distribution classes all
provide static methods which do have the concept of a default engine. This is described in more detail below.
CLHEP::HepRandom
Mu2e users should not use HepRandom; use the distribution classes instead.
The class CLHEP::HepRandom has a long history behind it. It was originally designed to be part of
Geant4 and is still used by Geant4 as its method for generating uniform random variates. Therefore its
design obeys constraints from the early days of Geant4 when the C++ standard,
the existing compilers and knowledge within the HEP community of C++ best practices were all immature.
In broad strokes HepRandom has the following properties:
- It is a singleton that holds a global instance of an engine;
- By default its underlying engine is HepJamesRandom.
- Calls to the
flat()method of HepRandom objects are passed through to the global instance of the engine. - It does not conform to a modern singleton pattern and most users will not recognize it as such. Using HepRandom can invoke dangerous, unexpected side effects.
- Its public interface does not exactly match that of a RandomEngine or that of any distribution; it is some sort of mixed thing.
- It is the base class for all distributions.
The discussion of the following code fragment will illustrate both the singleton behavior of HepRandom and that it does not conform to a modern singleton design pattern:
HepRandom ran1; double x1 = ran1.flat(); long seed(1234); HepRandom ran2(seed); double x2 = ran2.flat();
In the above, the syntax of C++ says that ran1 and ran2 are two independent instances of HepRandom
and naively one would expect them to be independent of each other. However they actually behave
very differently. If the HepRandom global instance of an engine does not already exist, instantiating ran1 will default
construct a HepJamesRandom engine. If the global instance of the engine already exists,
instantiating ran1 changes nothing.
The call to ran1.flat() will invoke the global instance to return a uniform random variate.
When ran2 is instantiated, it will set the seed of the global instance of the engine;
therefore instantiating ran2 changes the sequence of random variates returned by ran1!
This is an example of a dangerous and unexpected side effect.
Using CLHEP Distributions in Mu2e Modules
State and Seeds of Engines
The HepJamesRandom engine can be seeded by specifying a single long on the closed domain [0,900000000]; each value of the seed initializes the engine to a state that will produce a unique and repeatable series of psuedo-random uniform variates. I am not certain of the length of each unique series but it is much, much longer than we need. The internal state of the engine, is much larger than this single seed, 202 unsigned longs. Most of the other engines have similar properties: a large internal state that can be initialized by a much smaller seed.
The seed can be set either in the constructor or by calling the setSeed method. In the Mu2e environment, users should never set the seeds of an engine; the RandomNumberGenerator service is responsible for managing seeding and state.
In order to save the state of the engine, at an arbitrary point in its sequence, the full internal state of the engine must be saved. The RandomEngine base class provides two sets of methods for saving and restoring the state:
// Save and restore to/from streams virtual std::ostream & put (std::ostream & os) const; virtual std::istream & get (std::istream & is); // Save and restore to memory. virtual std::vector<unsigned long> put () const; virtual bool get (const std::vector<unsigned long> & v);
The RandomNumberGenerator service uses these methods to save the state of its engines either to the event or to a disk file.
Distribution with and without State
Distributions may have three sorts of state:
- The state of their associated engines.
- Static state that is defined at constructor time.
- State that changes on each call.
An example of the static state defined at constructor time is the range ]a,b[ of the random variate returned by RandFlat. Another example is RandGaussQ which functions by interpolation into a table; the table data occupies about 5 kB and is created at constructor-time.
Only a few distributions have the third kind of state, an example of which is found in RandGauss. When one first calls the fire() method of RandGauss, it computes two random variates, returns one and caches the second. On the second call it returns the cached value and does no further computation. On the third call it computes two values, returns one and caches the second. And so on. RandPoisson and the random bit functions of RandFlat also have this kind of state.
The classes RandPoissonT, RandPoissonQ, RandGaussT, RandGaussQ do not have the third kind of state; all of these are table driven so they have large state of the second kind. In both cases the Q versions are a little less accurate but compute much faster than either the T versions or the base versions. Although the Q versions are a little less accurate they have more than enough accuracy for Mu2e.
When a distribution has only state of the first and second kind then, when one wishes to save the state of the distribution, it is sufficient to save the state of the engine. When a distribution also has state of the third kind then it is necessary to also save this additional state. All of the stateful distributions have save and restore methods for this distribution-specific state. When designing the RandomNumberGenerator service we considered having it manage the state of distributions in addition to that of engines, with a mandate that, for distributions, it save state of the third kind. After some thought we decided in favor of a simpler solution: no Mu2e code will be allowed to use state-full distributions. Therefore, to ensure reproducibility, it is sufficient for the RandomNumber service to save the state of the engines.
The summary of this section is that Mu2e code should user RandGaussQ instead of RandGauss, RandPoissonQ instead of RandPoisson and RandBit instead of the random bit methods of RandFlat. There is an insignificant loss in accuracy with this choice but the upside is that it will be significantly easier to ensure repeatability.
Fire and Shoot
All of the CLHEP distribution classes have two sort of member functions that return random variates, one group contains the string "fire" in their name and the other group contains the word "shoot". All of the "fire" member functions are non-static member functions while all of the "shoot" member functions are static member functions.
When you construct a distribution object you must provide an engine as one of the constructor arguments. When you call one of the "fire" member functions it uses this engine. On the other hand, when you call one of the static "shoot" member functions it uses the CLHEP singleton engine. Consider the code fragment below:
// Get the engine associated with this module instance. art::Service<RandomNumberGenerator> rng; engine = rng->getEngine(); CLHEP::RandGaussQ gauss(engine); double x1 = gauss.fire(); double x2 = CLHEP::RandGaussQ::shoot();
Both x1 and x2 are random variates drawn from a unit Gaussian. The computation of x1 uses
the engine supplied by the RandomNumberGenerator service, while the computation of x2
uses the engine inside the HepRandom singleton. With the exception of code written for G4,
Mu2e user code should not use the static methods; they should use the per module engine that
is provided by the RandomNumberGenerator service. If you use the shoot() methods, your code will depend
on which other modules are present in the job and the order in which they are called!
G4
GEANT4 uses the static instances of the CLHEP random number generators both directly and through one level of indirection. In the G4 header Randomize.h, the following macros are defined:
#define G4RandGauss CLHEP::RandGaussQ #define G4UniformRand() CLHEP::HepRandom::getTheEngine()->flat()
Code in G4 uses these as,
double xf = G4UniformRand(); double xg = G4RandGauss::shoot();
I believe that the original intention was that all G4 code would use these macros, which
would make it easy to move to another random number package, either by redefining the macros
or by replacing them with adapter classes. Inspection of the G4 source, however, shows that there are
some places that directly use CLHEP::RandFlat::shoot(), CLHEP::Exponential::shoot() etc. .
All of that code uses the static engines via the shoot method; so this code should be repeatable.
Moreover there appears to be no use of the distributions that have time dependent state.
So G4 should be repeatable if
we manage the state of the engine inside the singleton HepRandom.
Most of the time Geant4 is repeatable if one properly sets the state of the CLHEP singleton engine at the start of each event. However there are times that this is not true. This occurs when the Geant4 team does not notice that one of the contributors has failed to follow the rules. When this happens we need to report it to the Geant4 team.
Aside: I have not yet figured out how G4 generates Poisson and Landau distributions. They do not appear to use the CLHEP versions.
RandGeneral
Suppose that you have an array of values that form a binned represention of a distribution. You can use RandGeneral to return a random variate drawn from that binned representation. Consider the code fragment below in which we define a parent distribution that is represented by 11 bins; the distribution is a triangle that ramps up and then down.
const int nbins(11);
double parent[nbins] = { 0.5, 1.5, 2.5, 3.5, 4.5, 5.5,
4.5, 3.5, 2.5, 1.5, 0.5 };
RandGeneral rgen0(parent,nbins);
RandGeneral rgen1(parent,nbins,1);
// Each of these will return a random variate on ]0,1[
double x0 = rgen0->fire();
double x1 = rgen1->fire();
The two instances of RandGeneral differ in the way that they interpolate within a bin; rgen0 assumes a uniform density across the bin while rgen1 assumes a delta function at the lower edge. RandGeneral always returns a variate on ]0,1[ and it is the user's responsibility to transform this into the domain native to the distribution.
In the figure below, the upper left plot shows a histogram of the parent distribution from the code fragment above.
In the upper right plot, the blue error bars show a binned histogram of the results
of 10,000 calls to rgen0->fire() this histogram has 44 bins, while the parent distribution had only 11.
The error bars are sqrt(n).
The parent distribution, scaled to 10,000 entries, is overlayed in red. In this figure one can see
that RandGeneral returns a constant density within each bin; it makes no attempt to smooth the distribution.
CLHEP does not provide a class that does a smoothed version of this, presumably because a fully general smoothing
algorithm is just too complicated. It is the user's responsibility to choose fine enough bins for
the job at hand.
In the lower left plot the blue error bars show a binned histogram of the results of 10,000 calls to
rgen1->fire() this histogram has 44 bins. The parent distribution, scaled to 10,000 entries is overlayed in red.
This illustrates that, when the IntType argument to the constructor of RandGeneral is set to 1, RandGeneral makes no attempt to interpolate within the bin and simply returns the lower edge of the bin. Careful inspection shows
that there is a bad interference between RandGeneral's notion of bin boundaries and the notion of bin boundaries
inside the histogramming package: the blue error bars are sometimes on the high side of the red vertical lines
and sometimes on the low side.
Notes for future developments.
The Old Style Method for Getting Seeds
As noted above, creating an engine involves specifying a seed value. Determining this value is at the discretion of the module creating the engine, and can be done in any of several manners. Here are some possibilities to get you started:
- Each CLHEP engine has a default seed value.
To specify the use of this default seed,
use the magic value -1 as the seed argument
in the
createEngine()call:createEngine( -1 );
- Specify a (non-negative) constant of your choice as the seed
argument in the
createEngine()call:createEngine( 13597 );
- Obtain a seed value from the module's
ParameterSet, typically with some fallback value in case theParameterSetomits the specified parameter:createEngine( pset.get<int>("seed",13597) );
- Obtain a seed value from the module's
ParameterSetvia a helper function,get_seed_value(), provided by art. Since this helper has defaults, each of the following calls has equivalent effect:createEngine( get_seed_value(pset) );createEngine( get_seed_value(pset,"seed") );createEngine( get_seed_value(pset,"seed",-1) );
Known Issues
- The mechanism for saving and restoring state does not work properly if a module consumes random numbers in begin/end of run/subrun or in file open/close call backs.
- The implementation is not thread safe.
- This is not an issue, just and FYI: CMS distributes seeds as part of the random number generator parameter set: they are distributed as pairs of (EngineId, Seed), where EngineId has a meaning similar to our case.